 Befehle
Pakete
Klassen
Strukturen
Fehlermeldungen
Befehle
Pakete
Klassen
Strukturen
Fehlermeldungen
Das dijkstra Paket (Version v0.12, 25. Juni 2020) kann zur Lösung des Dijkstra Algorithmus für gewichtete Graphen, gerichtet oder ungerichtet verwendet werden.[1] Das Paket selbst kann nicht zum Zeichen der Graphen genutzt werden, es führt die entsprechenden Schritte der Berechnung durch und gibt diese Schritte in der Form einer Tabelle aus. Daneben gibt es noch die Möglichkeit sich die Distanz und den Verbindungspfad zwischen den zwei betrachteten Punkten ausgeben zu lassen. Die Graphen können zum Beispiel mithilfe des Paketes adigraph beziehungsweise mit den Paket tkz-graph gezeichnet werden. Alternativ kann der Graph auch manuell mit tikz beziehungsweise innerhalb der picture Umgebung gesetzt werden.
Das Paket wird mit \usepackage{dijkstra} eingebunden und bindet seinerseits das simplekv Paket ein. Zur Zeit verfügt das Paket über keine Optionen.
Der Befehl \readgraph{...} wird verwendet um die Adjazenzliste eines ungerichteten Graphen, hier die benachbarten Knoten und die Gewichte der Kanten einzugeben. Im Fall eines gerichteten Graphen wird anstelle des Befehls \readgraph{...} der Befehl \readgraph*{...} verwendet. Dabei ist zu beachten, dass nur ganze positive Zahlen verwendet werden können.
Nachdem der Graph eingegeben wurde, wird mit dem Befehl \dijkstra{Start Knoten}{Ende Knoten} die Tabelle, mit den Ergebnissen des Dijkstra Algorithmus erstellt und ausgegeben. Anhand der gleichen Daten (Graph) kann mit dem Befehl \dijkdist die Distanz und mit dem Befehl \dijkpath der Pfad zwischen dem Start und dem Ende Knoten ausgeben werden.
Das nachfolgende Beispiel zeigt einen ungerichteten Graph mit den Knoten V = {A,B,C,D,E,F} und den Kanten E = {{A,B},{A,D},{B,C},{B,E},{B,F},{C,D},{C,F},{D,E},{E,F}}, und seine Repräsentation mit Hilfe von Adjazenzlisten.
| Graph | Adjazenzlisten |
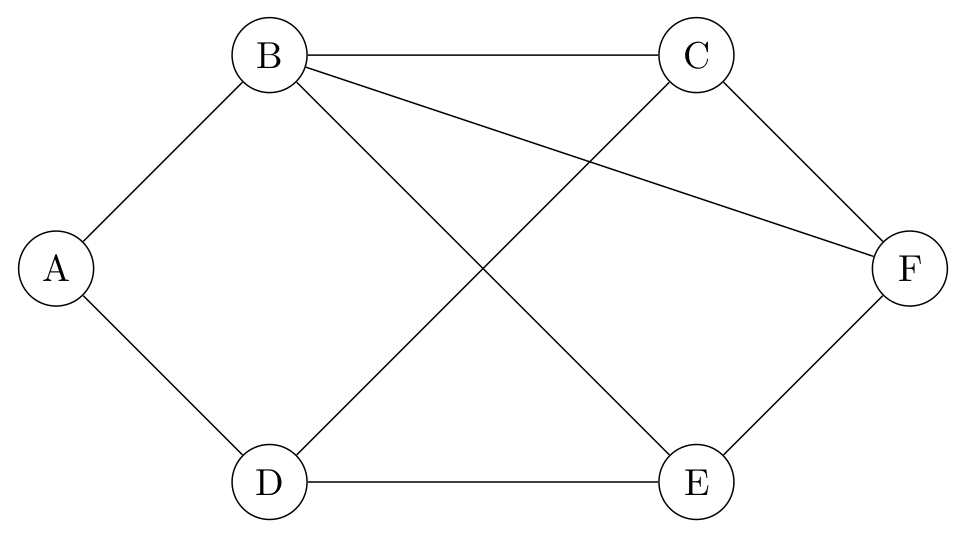 |
A: B, D B: C, E, F C: D, F D: E E: F |
In der folgenden Abbildung wurde die Kanten mit einer Gewichtung versehen. Anhand der Adjazenzlisten und der Gewichtungen der Kanten wurden dann die entsprechenden Werte im \readgraph{...} Befehl gesetzt.
| Graph | readgraph Befehl |
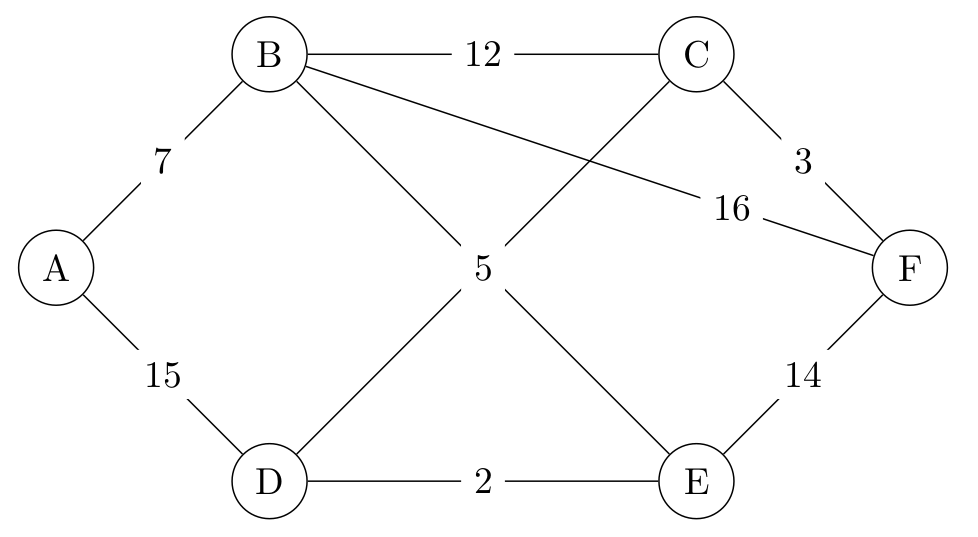 |
\readgraph{ A [B=7, D=15], B [C=12, E=4, F=16], C [D=5, F=3], D [E=2], E [F=14]} |
Nachdem die Werte des Graphen durch den readgraph Befehl für die Berechnung zur Verfügung gestellt worden sind, kann diese mit dem \dijkstra{Start Knoten}{Ende Knoten} Befehl durchgeführt werden. Als Start Knoten wird der Knoten A und als Ende Knoten der Knote F gewählt. Neben der Berechnungstabelle sollen auch der Abstand und der Pfad zwischen den zwei Knoten A und F ausgegeben werden.
| Ausgabe | Eingabe | ||||||||||||||||||||||||||||||||||||||||||
Pfad = A-B-E-D-C-F |
\begin{center}
Tabelle \\
\dijkstra{A}{F}
\end{center}
Distanz A-F = \dijkdist\\
Pfad = \dijkpath
|
Im Fall eines gerichteten Graphen werden anstelle der Nachbarknoten die Nachfolger erfasst. Und anstelle des Befehls \readgraph{...} wird die Stern Variante des Befehls \readgraph*{...} verwendet. Die drei anderen Befehle \dijkstra, \dijkdist und \dijkpath können wie gewohnt verwendet werden. Anhand des nachfolgenden Haus des Nikolaus wird die Funktionsweise im Fall eines gerichteten gewichteten Graphen gezeigt. Die gesuchte Verbindung liegt dabei zwischen den Knoten D und C.
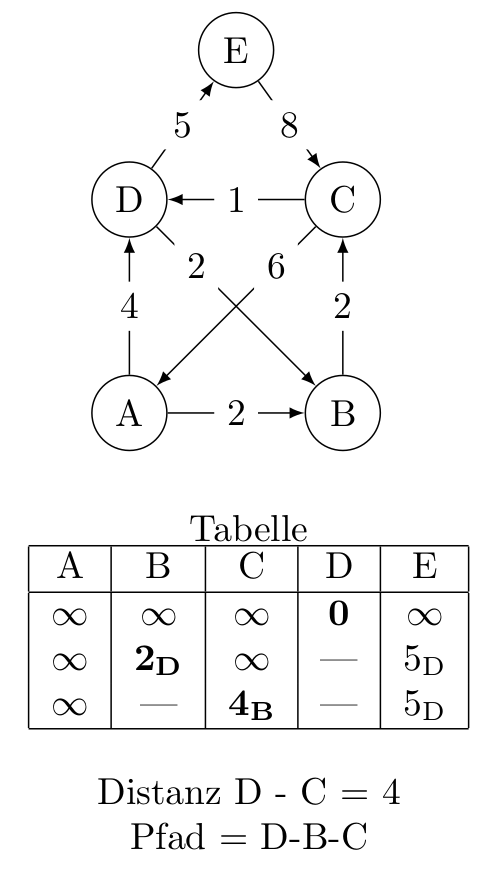
|
\documentclass{article}
\usepackage[utf8]{inputenc}
\usepackage{dijkstra}
\usepackage{adigraph}
\begin{document}
\NewAdigraph{Nikolaus}{
A:0,0;
B:2,0;
C:2,2;
D:0,2;
E:1,3.4}{
A,B:2; B,C:2;
C,A:6::near start; A,D:4;
D,E:5; E,C:8;
C,D:1; D,B:2::near start;
}
\begin{center}
\Nikolaus{}\par
\bigskip
\readgraph*{
A [B=2, D=4],
B [C=2],
C [A=6, D=1],
D [E=5, B=2],
E [C=8]}
Tabelle \\
\dijkstra{D}{C}\\ \bigskip
Distanz D - C = \dijkdist\\
Pfad = \dijkpath
\end{center}
\end{document}
|
Das Paket bietet eine große Auswahl an Optionen zur Gestaltung der Ausgabe der Tabelle.
Das Zeichen der Graphen ist für die Berechnungen nicht notwendig, es diente hier der Illustration.
Auch wenn hier für die Zeichnungen des adigraph Paket verwendet worden ist, sind die Berechnung unabhängig von diesem Paket erfolgt, es diente alleine der Darstellung der Graphen. Ob und wie die Graphen gezeichnet werden hat keinen Einfluss auf die Berechnung.